Relações Trigonométricas
A Trigonometria está relacionada a
diversas áreas do conhecimento humano, na Matemática está ligada
ao triângulo retângulo, triângulo qualquer e ao círculo
trigonométrico.
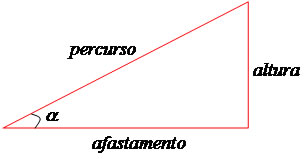
Observe um modelo de apresentação e
explicação das relações trigonométricas:
ângulo
α mais íngreme será a rampa, e quanto menor o ângulo menos
íngreme a rampa. Ressalte que todas as medidas estão relacionadas
entre si, da seguinte forma: altura x percurso, altura x afastamento
e afastamento x percurso. Destaque que para cada valor do ângulo de
inclinação existe uma determinação para os elementos, percurso,
altura e afastamento.
Dessa forma temos que em relação ao ângulo α:
Dessa forma temos que em relação ao ângulo α:
altura = cateto oposto
afastamento = cateto adjacente
percurso = hipotenusa
Com base nessa ideia devemos
determinar as seguintes relações trigonométricas:


EXEMPLO
EXERCÍCIOS
1. Edney está distante 50metros da base de uma torre. Com auxílio de
transferidor ele aponta para o topo dessa torre formando um ângulo de
40°. Qual a altura dessa torre?
Sen 40°= 0,64; Cos 40° = 0,76 e tg 40° = 0,83
a) 81,5m
b) 72,5m
c) 68,4m
d) 41,5m
2. Um funcionário de um circo estende uma corda de 35 metros a partir do
mastro. Sabendo que esse mesmo funcionário está distante 25m do centro
do circo, e que o ângulo formado entre o homem e o topo da base é de
50°, qual a altura do mastro?
Sen 50°= 0,76; Cos 50° = 0,64 e tg 50° = 1,19
a) 30m
b) 29m
c) 25m
d) 19m
EXERCÍCIOS
1) Calcular os catetos de um triângulo retângulo cuja hipotenusa mede 6 cm e um dos ângulos mede 60°.
2)
Quando o ângulo de elevação do sol é de 65º, a sombra de um
edifício mede 18 m. Calcule a altura do edifício.
(sen
65º = 0,9063, cos 65º = 0,4226 e tg 65º = 2,1445)
3. Quando o ângulo de elevação do sol é de 60º,a sombra de uma árvore mede 15m. Calcule a altura da árvore, considerando√3 = 1,7.
3. Quando o ângulo de elevação do sol é de 60º,a sombra de uma árvore mede 15m. Calcule a altura da árvore, considerando√3 = 1,7.
4.
Uma escada encostada em um edifício tem seus pés afastados a 50 m
do edifício, formando assim, com o plano horizontal, um ângulo de
32º. A altura do edifício é aproximadamente: (sen 32º = 05299,
cos 32′ = 0,8480 e tg 32º = 0,6249)
a)
28,41m
b) 29,87m
c) 31,24 m
d) 34,65 m
b) 29,87m
c) 31,24 m
d) 34,65 m
5)
Um avião levanta vôo sob um ângulo de 30º. Depois de percorrer 8
km, o avião se encontra a uma altura de:
a) 2
km
b) 3 km
c) 4 km
d) 5 km
6) Um foguete é lançado sob um ângulo de 30º. A que altura se encontra depois de percorrer 12 km em linha reta?
Nenhum comentário:
Postar um comentário